GMM(Gaussian mixture model) 混合高斯模型在机器学习、计算机视觉等领域有着广泛的应用。其典型的应用有概率密度估计、背景建模、聚类等。
2. GMM介绍
高斯混合模型(Gaussian Mixed Model)指的是多个高斯分布函数的线性组合,理论上GMM可以拟合出任意类型的分布,通常用于解决同一集合下的数据包含多个不同的分布的情况。
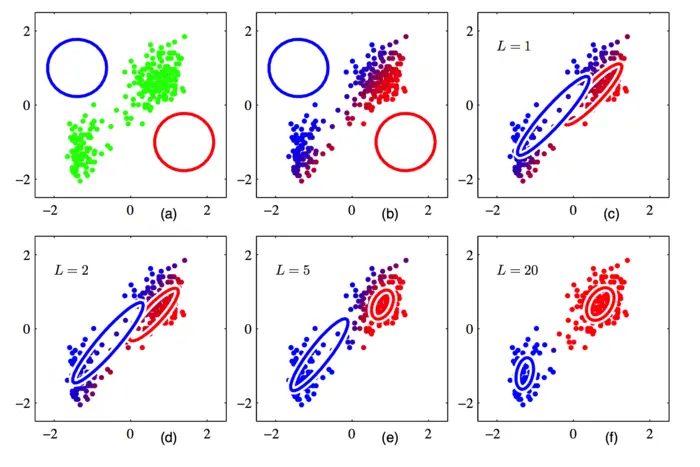
3. GMM原理解析
根据我们之前EM算法-原理详解,我们已经学习了EM算法的一般形式:
[Q_i(z^{(i)}) = P( z^{(i)}|x^{(i)}, heta^{j});;;;(1)
]
[sumlimits_{z}Q_i(z^{(i)}) =1
]
[L( heta, heta^{j}) = sumlimits_{i=1}^msumlimits_{z^{(i)}}Q_i(z^{(i)})log{P(x^{(i)},z^{(i)}| heta)}
]
现在我们用高斯分布来一步一步的完成EM算法。
设有随机变量(oldsymbol{X}),则混合高斯模型可以用下式表示:
[p(oldsymbol{x}|oldsymbol{pi},oldsymbol{mu},oldsymbol{Sigma})=sum_{k=1}^Kpi_kmathcal{N}(oldsymbol{x}|oldsymbol{mu}_k,oldsymbol{Sigma}_k)
]
[sum_{k=1}^Kpi_k=1
]
[0<pi_k<1
]
其中(mathcal{N}(oldsymbol{x}|oldsymbol{mu}_k, oldsymbol{Sigma}_k))称为混合模型中的第(k)个分量(component)。可以看到(pi_k)相当于每个分量(mathcal{N}(oldsymbol{x}|oldsymbol{mu}_k, oldsymbol{Sigma}_k))的权重
3.1 引入隐变量
我们引入一个隐变量(z_{ik}),(z_{ik})的含义是样本(x_i)来自第(k)个模型的数据分布。
[z_{ik}=
left {egin{array}{cc}
1, & if data item i comes from component k\
0, & otherwises
end{array}
ight.
]
则有
[P(x,z|oldsymbol{mu}_k, oldsymbol{Sigma}_k) = prod_{k=1}^Kprod_{i=1}^N[pi_kmathcal{N}(oldsymbol{x}|oldsymbol{mu}_k, oldsymbol{Sigma}_k)]^{z_{ik}}=prod_{k=1}^Kpi_k^{n_k}prod_{i=1}^N[mathcal{N}(oldsymbol{x}|oldsymbol{mu}_k, oldsymbol{Sigma}_k)]^{z_{ik}};;;;(2)
]
其中(n_k=sumlimits_{i=1}^Nz_{ik}),(sumlimits_{k=1}^Kn_k=N)
再对(2)进一步化简得到:
[P(x,z|oldsymbol{mu}_k, oldsymbol{Sigma}_k)=prod_{k=1}^Kpi_k^{n_k}prod_{i=1}^N[frac{1}{sqrt{2pi}oldsymbol{Sigma_k}}exp(-frac{{(x_i-oldsymbol{mu}_k})^2}{2oldsymbol{Sigma}_k})]^{z_{ik}}
]
取对数log后:
[logP(x,z|oldsymbol{mu}_k, oldsymbol{Sigma}_k)=sum_{k=1}^Kn_klogpi_k+sum_{i=1}^Nz_{ik}[log(frac{1}{sqrt{2pi}})-log(oldsymbol{Sigma_k})-frac{{(x_i-oldsymbol{mu}_k})^2}{2oldsymbol{Sigma}_k}]
]
3.2 确定E步极大似然函数
计算最大似然估计(L( heta, heta^{(j)})),(j)是第(j)次EM的过程,下式子中的(E_Q)是(1)中(Q)函数的期望值
[L( heta, heta^{(j)})=E_Q[logP(x,z|oldsymbol{mu}_k, oldsymbol{Sigma}_k)]
]
[L( heta, heta^{(j)})=E_Q[sum_{k=1}^Kn_klogpi_k+sum_{i=1}^Nz_{ik}[frac{D}{2}log(2pi)-frac{1}{2}log(oldsymbol{Sigma_k})-frac{{(x_i-oldsymbol{mu}_k})^2}{2oldsymbol{Sigma}_k}]]
]
[L( heta, heta^{(j)})=sum_{k=1}^K[sum_{i=1}^N(E_Q(z_{ik}))logpi_k+sum_{i=1}^NE_Q(z_{ik})[frac{D}{2}log(2pi)-frac{1}{2}log(oldsymbol{Sigma_k})-frac{{(x_i-oldsymbol{mu}_k})^2}{2oldsymbol{Sigma}_k}]]
]
我们记(gamma_{ik}=E_Q(z_{ik})),(n_k=sumlimits_{i=1}^Ngamma_{ik})可以算出
[L( heta, heta^{(j)})=sum_{k=1}^Kn_k[logpi_k+(frac{D}{2}log(2pi)-frac{1}{2}(log(oldsymbol{Sigma_k})-frac{{(x_i-oldsymbol{mu}_k})^2}{2oldsymbol{Sigma}_k})]
]
因为(frac{D}{2}log(2pi))是常数,忽略不计
[L( heta, heta^{(j)})=sum_{k=1}^Kn_k[logpi_k-frac{1}{2}(log(oldsymbol{Sigma_k})+frac{{(x_i-oldsymbol{mu}_k})^2}{oldsymbol{Sigma}_k})]
]
[gamma_{ik}=frac{pi_kmathcal{N}(oldsymbol{x}|oldsymbol{mu}_k,oldsymbol{Sigma}_k)}{sum_{k=1}^Kpi_kmathcal{N}(oldsymbol{x}|oldsymbol{mu}_k,oldsymbol{Sigma}_k)}
]
3.3 确定M步,更新参数
M步的过程是最化大(L( heta, heta^{j})),求出( heta^{(j+1)})
[ heta^{j+1} = arg max limits_{ heta}L( heta, heta^{j})
]
因为有
[n_k=sum_{i=1}^Ngamma_{ik}
]
通过(L( heta, heta^{j}))对(mu_k),(Sigma_k)求偏倒等于0得到
[mu_k=frac{1}{n_k}sum_{i=1}^Ngamma_{ik}x_i
]
[Sigma_k=frac{1}{n_k}sum_{i=1}^Ngamma_{ik}(x_i-mu_k)^2
]
[pi_k=frac{n_k}{N}
]
4. GMM算法流程
输入:观测数据(x_1,x_2,x_3,...,x_N)
输出:GMM的参数
- 初始化参数
- E步:根据当前模型,计算模型(k)对(x_i)的影响
[gamma_{ik}=frac{pi_kmathcal{N}(oldsymbol{x}|oldsymbol{mu}_k,oldsymbol{Sigma}_k)}{sum_{k=1}^Kpi_kmathcal{N}(oldsymbol{x}|oldsymbol{mu}_k,oldsymbol{Sigma}_k)}
]
- M步:计算(mu_{k+1},Sigma_{k+1}^2,pi_{k+1})。
[n_k=sum_{i=1}^Ngamma_{ik}
]
[mu_{k+1}=frac{1}{n_k}sum_{i=1}^Ngamma_{ik}x_i
]
[Sigma_{k+1}^2=frac{1}{n_k}sum_{i=1}^Ngamma_{ik}(x_i-mu_k)^2
]
[pi_{k+1}=frac{n_k}{N}
]
- 重复2,3两步直到收敛
